Volume¶

class pyvsim.Primitives.Volume(dimension=array([1, 1, 1]), fastInit=False)[source]¶

This is another convenience class an hexahedron. Most methods, however, only work if the faces of the hexa are planar

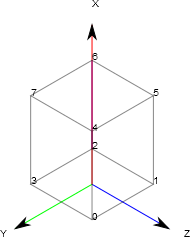
The point numbering convention and orientation is given in the figure below:

Methods

connectivity = None¶

The connectivity of the hexa is defined so that triangle normals always point outside the volume. This is important for ray tracing.

expand(factor)[source]¶

Offsets each point of the volume by a multiplicative “factor” in the direction of the centerpoint.

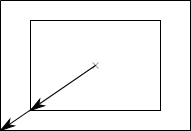
The procedure is shown in the figure below:

The original vector (\(V_o\)) and the resulting vector (\(V_r\)) are related by the factor \(f\) as:

\(V_r = V_o \cdot f\)

Parameters :	factor : float The offset factor

interpolate(p, verify=True)[source]¶

This is a convienience function to interpolate the data in the ”.data” field of this object. As the field is not under surveillance, it is the responsibility of the user to ensure that the field contains a numpy.ndarray with the shape \((M,8)\), i.e. one data point for each vertex

Parameters :	p : numpy.ndarray \((N,3)\) A collection of points verify : boolean (True) Verifies if the point is contained in the hexa defined by the edges. If not, the corresponding row of result will be zeroed out
Returns :	result : numpy.ndarray \((N,M)\) An array with the data from the field ”.data” interpolated

parametricToPhysical(p)[source]¶

Transforms a vector or a list of vectors in parametric coordinates with the following properties:

\(\left( x,y,z \right) \mapsto \left(u,v,w \right)\)

Where \(x,y,z\) are world coordinates and \(u,v,w\) are parametric coordinates defined so that:

\(0 \leq u,v,w \leq 1\)

represents a point inside the volume.

physicalToParametric(c)[source]¶

Transforms a vector or a list of vectors in parametric coordinates with the following properties:

\(\left( x,y,z \right) \mapsto \left(u,v,w \right)\)

Where \(x,y,z\) are world coordinates and \(u,v,w\) are parametric coordinates defined so that:

\(0 \leq u,v,w \leq 1\)

represents a point inside the volume.

pointInHexa(p)[source]¶

This is intended as a lightweigth test for checking if a point (or a set of them) lies inside an hexahedron. This uses the algorithm implemented in Utils.

Parameters :	p : numpy.ndarray \((N,3)\) A collection of points
Returns :	result : numpy.ndarray \((N)\) An array with “1” corresponding to points in the hexa or “0” otherwise