Part¶

class pyvsim.Primitives.Part[source]¶

This implementation of the Component class is the representation of a surface using triangle elements.

This is supposed to be the standard element in pyvsim, as raytracing with such surfaces is relatively easy and plotting is also made easy by using libraries such as VTK, Matplotlib and OpenGL.

Another benefit is the possibility of directly reading this topology from a STL file, that can be exported from a CAD program.

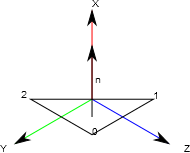
It is important to notice that the triangle definition defines a series of behaviors within pyvsim, such as defining whether a ray is entering or leaving a body.

The definition of a triangle is given in the figure below:

And it is important to remember that in a closed surface, the normal always points outwards.

Methods

bounds[source]¶

Returns the coordinates of the aligned-to-axis-bounding box

Returns :	bounds : numpy.ndarray \((6)\) An array with the following data [xmin, xmax, ymin, ymax, zmin, zmax]. Defining a box aligned to axis bounding the Part

clearData()[source]¶

Implement this method whenever your object possesses geometrical features that are calculated from their interaction with the ambient (e.g. - any raytraced features). This method is called after all spatial transformations

color = None¶

Part color

connectivity = None¶

The connections between points defining triangles. Given as an \((N,3)\) array of indexes of points. The order of definition affects the direction of the triangle normal

data = None¶

Field for storing extra data about the part

intersections(p0, p1, tol=1e-08)[source]¶

This is a method used specifically for ray tracing. The method returns data about the first intersection between line segments and the polygons defined in the Component. The implementation of the intersection is given by the inheriting classes.

This method is intended for use in raytracing algorithms, as there is an initial, fast verification to see if there is a chance of any triangle in the polygon to be intersected, then, if it is the case, it executes expensive search.

Special cases when intersecting with individual triangles:

• if line is contained on triangle plane, will ignore
• if intersection is at p0, will not return p0

Algorithm adapted from http://geomalgorithms.com/a06-_intersect-2.html

Parameters :

p0, p1 - numpy.ndarray :math:`(N,3)` : Coordinates defining N segments by 2 points (each p0, p1 pair), which will be tested for intersection with the polygons defined in the structure. tol - double : Tolerance used in the criteria for intersection (see documentation of each implementation)

Returns :

None : If no intersections are found. Otherwise returns a list with: lineParameter : This is used to indicate how far the intersection point is from the segment starting point, if 0, the intersection is at p0 and if 1, the intersection is at p1 Iff the parameter is > 1 (999), no intersection was found intersectionCoordinates : This is where the intersections are found triangleIndexes : This is the index of the triangle where the intersection was found. If no intersection found, will return 0, but attention, the only way to guarantee that no intersection was found is when the lineParameter is zero. normals : The normal vector at the intersection point (if the surface is defined with normals at vertices, interpolation is performed). part : A list with references to this object. This is, in this case, redundant, but that makes the function signature uniform with the Assembly class

material = None¶

Material of the part (initialized as IdealMaterial(1))

normals = None¶

Stores each triangle normal vector in a \((N,3)\) array

opacity = None¶

Part opacity

points = None¶

A \((N,3)\) array containing the coordinates of the part points

refractiveIndex(wavelength=5.32e-07)[source]¶

Returns the index of refraction of the material given the wavelength (or a list of them)

Parameters :	wavelength : scalar or numpy.ndarray The wavelength of the incoming light given in meters
Returns :	refractiveIndex : same dimension as wavelength The index of refraction

rotateImplementation(angle, axis, pivotPoint)[source]¶

This method is in charge of updating the position of the point cloud (provided it exists) when the Part is rotated.

There is an exception handling because there is the possibility that the part is translated before the points are defined. This is extremely unlikely, but should not stop the program execution.

In case the surface is defined with normals on vertices (thus making self.normals not None), these vectors are rotated.

Parameters :	angle : Angle : scalar (in radians) axis : numpy.ndarray \((1,3)\) Vector around which the rotation occurs. pivotPoint : numpy.ndarray \((1,3)\) Point in space around which the rotation occurs. If not given, rotates around origin.

surfaceProperty = None¶

Surface property (initialized as Component.OPAQUE)

translateImplementation(vector)[source]¶

This method is in charge of updating the position of the point cloud (provided it exists) when the Part is translated.

There is an exception handling because there is the possibility that the part is translated before the points are defined. This is extremely unlikely, but should not stop the program execution.

Parameters :	vector : numpy.ndarray \((1,3)\) Vector to translate the component. An array with x, y and z coordinates

visible = None¶

Toggles visibility